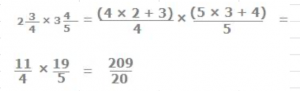In this page, we will learn:
- How to multiply fractions which are both proper and improper fractions
- How to multiply fractions and a whole number
- How to multiply mixed numbers
In each of the above three types of how to multiply fractions, apply the following rule:
![]()
Type 1: How to multiply fractions which are proper fractions.
Proper fractions are those in which numerators are less than denominators.
So, (3/5) × (4/7) = (3 × 4)/ (5 × 7) = 12/35
Note:
Divide both numerator and denominator by the highest common factor (hcf) that they may have.
For example:
In (3/5) × (10/8) which is equal to 30/40, in the final product 30/40, the numerator 30 and the denominator 40 have common factors. Divide each by their hcf to reduce the final product to the simplest terms. Now 30 = 3 × 10, and 40 = 4 × 10. Therefore, divide them both by this hcf, 10 to reduce the fraction into the simplest form.

Type 2: How to multiply fractions which are improper fractions
Fractions in which numerators are bigger than denominators are called improper fractions. Apply the same rule.
Example:
![]()
(6/5) × (9/8) = (6 × 9)/ (5 × 8) = 54/40
Now, what is the HCF of 54 and 40?
54 = 2 × 27 = 2 × 3 × 3 × 3, and 40 = 2 × 20 = 2 × 2 × 10 = 2 × 2 × 2 × 5 =
Now, the hcf of 54 and 40 is 2
So, 54/40 = (2 × 27)/ (2 × 20) = 27/20
Note:
In writing 54/40 as 27/20, one of the two below is done:
Divide both 54 and 40 by their hcf, 2 as:
(54 ÷ 2/40 ÷ 2) = 27/20, or in (2 × 27)/ (2 × 20), we say “the common factor 2 is cancelled”, which step is shown as: (2 × 27)/ (2 × 20) = 27/20
Type 3: How to multiply fractions and a whole number
Example:
3 × (4/15) =
We can rewrite the whole number 3 as an improper fraction 3/1, but this is not always necessary.
(3/1) × (4/15) = (3 × 4)/ (1× 15) = 12/15
We could also straight away write:
3 × (4/15) = (3 × 4)/15 = 12/15
Once again, what is the hcf of 12 and 15?
12 = 3 × 4 and 15 = 3 × 5, so 12/15 = (3 × 4)/(3 × 5) = 4/5
Type 4: How to multiply fractions obtained from mixed numbers.
Example: