1. What is the Binomial Expression?
Any expression that has two terms is called a binomial expression.
Eg: x + y, x + 2, 2x + y, 3x + 4y, 3x² + 4y³.
2. Binomial Expansion for any positive integral index:
Consider the algebraic formulas that are listed below to arrive at the Binomial Theorem
( x + y )1 = x + y
( x + y )2 = x2 + 2xy + y2
( x + y )3 = x3 + 3×2 y + 3xy2 + y3
(x + y )4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
(x + y )5 = x5 + 5x4y + 10×3 y2+ 10x2y3 + 5xy3 + y5
Now, let us make the following observations based on the above 5 algebraic formulas:
1. The coefficients in each of the above binomial expansions follow a pattern. The pattern can be understood with Pascal’s triangle as follows:
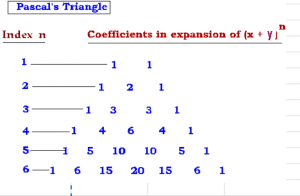
2. First let us become familiar with the values of the binomial coefficients
(see point no. 4 in red below for a detailed discussion of binomial coefficients)
Remember the Combinations Formula ncr ?
It is

and use it to write the following sample values in the binomial expansion no.5 above:
5c0 = 1, 5c1 = 5, 5c2 = 10,5c3 = 10, 5c4 = 5, 5c5 = 5
3. The first term in each of the above binomial expansions is xn or nC0 xn
The second term in the above expansions is nxn-1
4. As the expansion proceeds the power of x decreases by one, while the power of y increases by one.
The number of terms in each of the expansion is (n+1). Note: the last term is (n + 1) th term, not nth term.
5. Generalizing the above properties in the above four algebraic expansions.
We can write the following general binomial theorem: let x and y be two real numbers and index n be a positive integer.
Then, the Binomial Theorem or Binomial Expansion of (x + y)n is (x+y)n = nc0.xn + nc1.xn-1 y + nc2.xn-2 y2 +nc3.xn-3 y3 +……. +ncr.xn-r yr +…. +ncn.yn
6. Number of terms in the binomial expansion: (x + y)n
The number of terms in the binomial expansion is always one more than the index n,
i.e., in a binomial expansion, number of terms = n + 1, where n is the index.
As the terms are written, the power of x decreases by one, while the power of y increases by one.