1. Trig Identities on the six trigonometric ratios:
(Note: trig is an abbreviation for trigonometric. We will use trig for the word trigonometric to avoid repetition and therefore boredom.)
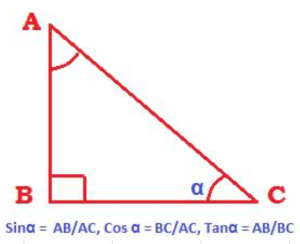
- Sinα = opposite side/hypotenuse = AB/AC
- Cosα = adjacent side/hypotenuse = BC/AC
- Tanα = opposite side/adjacent side = AB/BC
2. The reciprocal Trig identities
- cosecα = 1/sinα
- secα = 1/cosα
- cotα = 1/tanα
3. The three Pythagorean trig identities
- Sin2α + Cos2α = 1
- Sec2α – tan2α = 1, Sec2α = 1+ tan2α
- Cosec2α – cotan2α = 1, Cosec2α = 1+ cotan2α
4. The quotient Trig identities:
- tan α = sin α /cos α
- cot α = cos α /sin α
5. Trig identities of negative angles:
- Sin (– α) = –sin α
- cos (– α) = cos α
- tan (– α) = – tanα
- cot (– α) = – cotα
- Sec (– α) = Sec α
- cosec (– α) = – cosec α
6. Trig identities of compound angles
- sin (A + B) = sinAcosB + cosAsinB
- sin (A – B) = sinAcosB – cosAsinB
- cos (A + B) = cosAcosB – sinAsinB
- cos (A – B) = cosAcosB + sinAsinB
- Tan(A + B) = (sinAcosB + cosAsinB)/(cosAcosB – sinAsinB)
- Tan(A – B) = (sinAcosB – cosAsinB)/(cosAcosB + sinAsinB)
7. Trig identities on products of compound angles
- sin(A + B)sin(A – B) = sin2A – sin2B Or cos2B – cos2A
- cos (A + B)cos(A – B) = cos2A – sin2B Or cos2B – sin2A
- tan (A + B)tan(A – B) = (tan2A – tan2B)/ (1 – tan2Atan2B)
- tan(A + B + C) = (tan A + tan B + tan C – tanA tanB tanC)/ (1– tanAtanB – tanB tanC –tanC tanA)
8. Trig identities on conversion of sum of angles to product of angles
- sin (A + B) + sin ( A – B) = 2sinAcosB
- sin (A + B) – sin (A – B) = 2 cosAsinB
- cos ( A + B ) + cos (A – B) = 2cosAcosB
- cos ( A – B ) – cos (A + B) = 2sinAsinB
9. Trig identities on sums of angles.
10. trig identities on double angles:
- Sin2A = 2sinAcosA Or 2tanA/ (1 + tan2A)
- cos2A = 2cos2A – 1 Or 1 – 2sin2A Or (1 – tan2A)/(1 + tan2A)
- tan2A = 2tanA/(1 – tan2A)
11. Trig identities on triple angles
- Sin3A = 3sinA – 4sin3A
- cos3A = 4cos3A – 3cosA
- tan3A = (3tanA – tan3A)/(1 – 3tan2A)
12. Trig identities on sub-multiple angles
- sin2A + sin2B + sin2C = 4sinAsinBsinC Or -1 – 4cosAcosBcosC
- cos2A + cos2B + cos2C = 1 – 4 sinAsinBsinC
- tan2A + tan2B + tan2C = tan2C tan2B tan2C
13. The law of sines Or the sine rule:
14. the law of cosines or the cosine rule
- a2 = b2 + c2 – 2bc cosA
- b2 = a2 + c2 – 2ac cosB
- c2 = b2 + a2 – 2abcosC
15. the projection formula
- a = bcosC + ccosB
- b = acosC + ccosA
- c = bcosA + acosB