A Ratio is an expression of comparing two similar quantities. To know or find, how many times one thing of one kind is greater (or smaller) than another of the same kind, a ratio is used. Suppose today, John is 50 years old and his son Tom 25 years. Then, to compare the ages of the father and son, a ratio may be applied as: 50:25:00. And, 50: 25 = 2: 1. From the ratio 2: 1, we say John is twice as old as his son today.
Note:
- Two dissimilar quantities are not compared using a ratio. For example, if John is 150 cms tall and Tom 120 lbs heavy, then height and weight are not compared using a ratio as they are not similar.
- Ratios are only expressed on similar quantities having same units. For example, the length of one line segment AB is 5 cms and the length of another line segment CD is 2 inches. Then, the ratio of the lengths of the two line segments is not 5: 2 as the units of length are not the same. First of all, express both the quantities in same units. Now, 1 inch is 2.5 cms. So, 2 inches is 2 × 2.5 cms, i.e 5 cms. Therefore, the ratio of the lengths of the two line segments is 5 cms: 5 cms = 1: 1.
- Ratios are always expressed in the lowest terms. (numbers in a ratio are in lowest terms, if their HCF is 1). The HCF of 150 and 120 is 30. After removing this HCF 30 (by dividing both the terms 150 and 120 with 30), the ratio in lowest terms is 5: 4.
1. TERMS OF A RATIO:
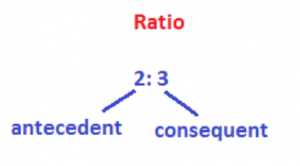
The two numbers in ratio are called terms of the ratio. In a ratio, the first term is called the antecedent and the second, the consequent. In the ratio 2: 3, 2 is the antecedent and 3 is the consequent.
2. TYPES OF RATIOS:
1. Duplicate Ratio:
If a: b is a ratio, then its duplicate ratio is a2: b2
Example:
If 2: 3 is a ratio, then its duplicate ratio is 22: 32 i.e. 4:9
2. Sub-duplicate Ratio:
If a: b is a ratio, then its sub-duplicate ratio is √ a: √b
Example:
If 16: 25 is a ratio, then its sub-duplicate ratio is √16: √25 = 4: 5
3. Triplicate Ratio:
If a:b is a ratio, then its triplicate ratio is a3: b3
Example:
If 2: 3 is a ratio, then its triplicate ratio is 23: 33 = 8: 27
4. Sub-triplicate Ratio:
If a: b is a ratio, then its sub-triplicate ratio is a1/3: b1/3
Example:
If 8: 27 is a ratio, then its sub-triplicate ratio is 81/3: 271/3; 81/3: 271/3 = (23)1/3: (33)1/3 = 2: 3
Inverse or Reciprocal Ratio: The inverse ratio of a: b is 1/a: 1/b
Example:
If 2: 3 is a ratio, then its inverse ratio is ½: 1/3