What length of a staff will measure two planks of length 36 cms and 48 cms exactly?
Answer:
It is a 12 cms long staff.
How to find?
In one way, like this:
Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36, and
Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 24, and 48.
Among the above factors of the two numbers, the highest factor common to both is 12. In another easier way, it is 36 = 12 × 3, and 48 = 12 × 4. 12 is the greatest factor common to 36 and 48. Therefore, the two planks 36 and 48 cms long are divided into 3 and 4 pieces respectively, each of length 12 cms. So, 12 divides both 36 and 48 exactly. We say, 12 is the highest common factor of 36 and 48.
Now, 36 = 4 × 9 = 22 × 32 and 48 = 3 × 16 = 24 × 3
Now, 2 and 3 are the common prime factors of 36 and 48. Next, to find the HCF (highest common factor) of 36 and 48, find the product of the least powers of the common prime factors 2 and 3.
It is 22 × 3 = 4 × 3 = 12.
So, there we have, 12 is the highest common factor of 36 and 48. This is called prime factorization of two numbers, i.e. expressing numbers as product of their prime factors. Prime factorization is a method for finding the HCF (highest common factor) of two numbers.
How to Find the HCF of two or more numbers:
How to Find HCF of Fractions:
HCF × LCM = a × b
1. HCF of Fractions:
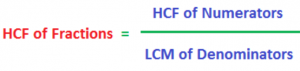
Find the HCF of 2/3 and 3/4.
Solution:
HCF of numerators 2 and 3 is 1, and LCM of denominators 3 and 4 is 12. Therefore, HCF of 2/3 and 3/4 is 1/12
2. Product of two numbers a and b = Product of HCF and LCM of a and b, i.e.
![]()
Consider two numbers 12 and 18.
12 = 22 × 3, and 18 = 2 × 32
Therefore, HCF of 12 and 18 is = 2 × 3 = 6, and LCM of 12 and 18 is = 22 × 32 = 36. Again, product of 12 and 18 is 12 × 18 = 216, and product of their HCF and LCM is 6 × 36 = 216.