What you will learn in this lesson on Exponents?
Exponents or Exponential form is an easy way of expressing a same number multiplied to itself one or more times. The exponential form of 3 × 3 is 32 and 32 is the short form for “3 multiplied by itself 2 times”. 2 × 2 × 2 is shortened as 23. 23 is exponential expression signifying that 2 is multiplied 3 times to itself. In 32, 3 is base and 2 is exponent. Base denotes the number that is multiplied to itself, while Exponent, number of times that the number is so multiplied. The product a × a × a × a × ……. n times is an in an, a is base and n is exponent.
Note:
a can be any number, but n is a natural number (the numbers that we use for counting)
a to the power 2 is called a squared.
For example,
3 to the power 2 written as 32 is called 3 squared.
a to the power 3 is called a cubed.
For example,
3 to the power 3 written as 33 is also called 3 cubed. If you wish to capture a terse overview of each Exponents Formula, then go through each of the following header-links. You can also click the header-links to take you to the page discussing in detail the specific Exponents concept:
Laws of Exponents:

Let a be not equal to 0. Then a0 = 1.
The negative sign of the base: remains if power is odd integer
Example: (-2)3 = – 8
Disappears, if power is even integer
Example: (-2)4 = 16
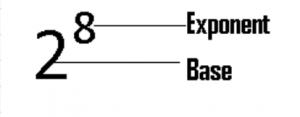
CONSIDER THE FOLLOWING PRODUCT OF 2 MULTIPLIED 8 TIMES WITH ITSELF.
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Is there an easier, shorter-form of writing or expressing the above long product? The answer is an emphatic and relieving Yes. It is 28, read as “2 to the power 8”. 28 is called the exponential form of 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2. In 28, 2 is called base and 8 is called exponent.

Note:
1. 52 is 5 to the power 2, but a special name is “5 squared”
2. 1003 is 100 to the power 3, but a special name is “100 cubed”
So, we see that there are special names in calling the exponential forms when the exponents are 2 and 3.
Example1:
1. Express 64 to base 2
Solution:
64 = 2 × 2 × 2 × 2 × 2 × 2 = 28 and read as “2 to the power 8”
2. Express -1/128 to base ½
Solution:
-1/128 = (-1/2) × (-1/2) × (-1/2) × (-1/2) × (-1/2) × (-1/2) × (-1/2) = (-1/2)7, and read as
“Minus one-by-two to the power 7”
Note:
1. – 8 = -2 × -2 × -2 = (-2)3 = – 8
2. 16 = 2 × 2 × 2 × 2 OR
-2 × -2 × -2 × -2 = (-2)4 = 16
From the above two examples, we note the following two very important rules: If the exponent is an odd integer, the negative sign of the base inside the brackets will not go away;
And if the exponent is an even integer, the negative sign of the base inside the brackets will go away. Let us summarize the above two points in blue in the table below:

Very Important Point:
Any number to the power 0 is equal to 1, i.e. a0 = 1, a is any number, except 0.
Negative Integral Exponents: If a is any number and n is a positive integer, then a –n = 1/an
For example,
2–2 = 1/22 = ¼
4 –3 = 1/43 = 1/64