What you will learn in this lesson on Ratio and Proportion?
A ratio is comparison of two similar quantities.
For example, number 10 is twice as large as 5. Now, a ratio can also be used to express this relation of ‘10 being double of 5’ as 10: 5, read as “10 is to 5”.
Also, the ratio 10: 5 can be written as a fraction 10/5 = 2. So, a ratio is a comparison tool. In general, the ratio of a to b is written as A ratio is a fraction. The ratio a: b as a fraction is
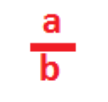
In the ratio 10: 5, the two numbers 10 and 5 are called terms of the ratio. Again, ratios are simplified. Ratios are simplified by cancelling out common factors in the terms of the ratio. Therefore, the ratio 10: 5 as a fraction is 10/5 = 2/1 = 2: 1. So, 10: 5 = 2: 1 after canceling out the common factor 5. A Ratio is not used to compare quantities of different units. For example, the ratio of 5 yards to 5 meters is not 5: 5, i.e not 1: 1, because yards and meters are not same units.
First, convert yards and meters into a same units: centimeters.
5 yards = 5 × 90 cms = 450 cms, and
5 meters = 5 × 100 cms = 500 cms.
So, the ratio of 5 yards to 5 meters is
450 cms: 500cms, i.e. 450: 500 = 9: 10
Now, if you wish to set off with your lesson on Ratio and Proportion in detail, then click on any of the links below: Or, if you wish to capture a terse overview of each Ratio and Proportion formula, then go through each of the following header-links. Or, you may as well click on the following header-links to take you to the page discussing in detail the specific Ratio and Proportion concept: Ratios are always expressed in lowest terms. 4: 6 is simplified to 2: 3 by canceling out the common factor 2 from the terms of the ratio. In a ratio, the order of the terms carries importance. A father is 40 years old and his son 10 years. The ratio of father’s age to his son’s age is 40: 10 = 4: 1 The father is 4 times as old as his son. But the ratio 1: 4 signifies the ratio of the son’s age to that of the father. In general, the ratio a: b is not the same as b: a, provided a ≠ b. Multiplying or dividing the terms of a ratio with a same number will not change the ratio. a: b is same as m × a: m × b for example, 2: 3 is same as 4 × 2: 4 × 3 = 2: 3 also, a: b is same as a/m: b/m for example, 4: 6 which is 2: 3 is same as 4/2: 6/2 = 2: 3
How to compare ratios?
Since ratios are fractions, comparing fractions will inherently compare ratios. Which of the two ratios 4: 7 or 8: 12 is greater?
Answer: 4: 7 is 4/7 and 8: 12 = 2: 3 is 2/3
Now, is 4/7 > 2/3?
Find cross product to compare fractions a/b < c/d, if a × d < b × c since, 4 × 3 < 7 × 2, therefore 4/7 < 2/3
How to divide a Whole Number into two parts whose ratio of division is given?
Let ![Rendered by QuickLaTeX.com 100 be divided between A and B in the ratio of 2: 3. Then the share of A = [2/ (2+3)] × 100 = 40, and share of B = [3/ (2+3)] × 100 = 60, or alternatively, easily and common-sensically, share of <em>B = 100 - 40 = 60.</em> <strong>How to find A: B: C, if A: B and B: C are given?</strong> Let A: B = 2: 3, and B: C = 4: 5, then A: B: C = 8: 12: 15 <img class="alignnone wp-image-388" src="http://blendedlearningmath.com/wp-content/uploads/2021/08/Снимок-экрана-2021-08-16-в-14.15.13-300x167.png" alt="Ratio of A:B:С" width="361" height="202" /> Mnemonic to find A: B: C is <strong>How to find A: B: C: D, if A: B and B: C and C: D are given? </strong>Mnemonic to find A: B: C: D IS <img class="alignnone wp-image-389" src="http://blendedlearningmath.com/wp-content/uploads/2021/08/Снимок-экрана-2021-08-16-в-14.15.17-239x300.png" alt="A:B=a:b" width="220" height="276" /> <strong>Proportion. </strong>Proportion is equality of two ratios. The ratio of 2 to 3 is same as the ratio of 4 to 6, i.e. <em>2: 3 = 4: 6</em> <strong>Therefore, the two ratios 2: 3 and 4: 6 are proportionate and written as:</strong> 2: 3:: 4: 6 and read as the ratio of 2 to 3 is same as that of 4 to 6. If 2: 3 = 4: 6, then 2 × 6 = 3 × 4, i.e. 12 = 12, i.e. A Very important rule: Let two ratios a: b and c: d be proportionate, i.e. a: b :: c : d (read as the ratio of a to b is same as that of c to d). In the proportion a: b :: c : d product of means = product of extremes. If a: b = c: d, then a × d = b × c <img class="alignnone wp-image-390" src="http://blendedlearningmath.com/wp-content/uploads/2021/08/Снимок-экрана-2021-08-16-в-14.15.23-300x139.png" alt="product of means" width="326" height="151" /> There are two types of proportion. They are Direct and Indirect proportion. <strong>Direct proportion. </strong>If the ratio of a to b is same as the ratio of c to d, i.e. the ratios a: b :: c: d, then a × d = b × c <strong>Example: if 3 pencils cost](https://blendedlearningmath.com/wp-content/ql-cache/quicklatex.com-b4cf3641e7edba7e9a8bcf60634a0055_l3.png) 30, then 5 pencils will cost what price?
30, then 5 pencils will cost what price?
Answer:
Set up a proportion as below: 3: 30:: 5: P, then 3 × p = 30 × 5, p = 50. Indirect proportion. If the ratio of a to b is inverse as the ratio of c to d, then a: b:: d: c, then a × c = b × d
Example: 2 men finish a work in 3 days, then 3 men will do the same work in how many days?
Answer: The ratio of 2 to 3 is indirect to the ratio of 3 to N, because more men take less days to finish a same work. So, the ratio to be set up is like this: The ratio of 2 to 3 is indirect to that of 3 to N, or 2 to 3 is same as that of N to 3. So, 2: 3 :: N: 3, 2 × 3 = N × 3, i.e. N = 2.