The quadratic formula is an alternative to solving a quadratic equation. To solve a quadratic equation means to find the roots of a quadratic equation. Roots of a quadratic equation are values of the variable in the quadratic equation, say x, which reduce the value of the equation to zero.
![]()
Now consider a quadratic equation of the standard form:
ax2 + bx + c = 0. We know a quadratic equation can be solved by the factoring method. But, not all trinomials in the form of a quadratic equation can be solved by the factoring method.
Consider for example the following equation:
x2 + 4x + 2 = 0. In this quadratic equation, the product of roots, which have yet to be solved for, is 1 × 2, i.e. 2. But what two integers can be there, having a product of 2, with a sum -4 and ax2 + bx + c = 0. None, indeed! Therefore, the need for an alternative for finding the roots of this quadratic equation arises. The alternative is called the “The Quadratic Formula” When factoring a quadratic equation gets difficult, then the quadratic formula enables us to find roots of a quadratic equation of the form ax2 + bx + c = 0. In this formula, x is roots of the quadratic equation ax2 + bx + c = 0
Derivation of the quadratic formula: Consider the quadratic equation ax2 + bx + c = 0. Now, ax2 + bx = – c
Divide both sides of the equation by a. So, x2 +( b/a) x =-c/a let us add b2/4a2 to both sides of above, so we get x2 +( b/a) x+ b2/4a2 = -c + (b2/4a2 ) factorize the perfect square trinomial in the left side, and apply LCM in the right (x + (b/2a))2 = (b2 – 4ac)/4a2
Take square roots on both sides, x + (b/2a) = ± [√(b2 – 4ac)/2a]. Finally, this is the solution to the general quadratic equation ax2 + bx + c. And the solution is called the quadratic formula.
Example 1:
Solve the quadratic equation x2 + 4x + 2 = 0
Solution :
As tried above, this quadratic equation cannot be solved by the factoring method. Therefore, let us use the quadratic formula derived above. Comparing the given quadratic equation x2 + 4x + 2 = 0 with the general form ax2 + bx + c. We see, a = 1, b = 4, c = 2. Now the roots of the quadratic equation x2 + 4x + 2 = 0, using the quadratic formula are
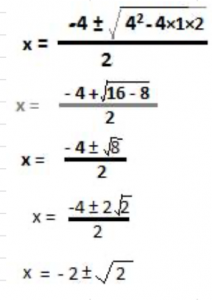
Now, square root of 2 is an irrational number, therefore factoring method could not work for finding roots of this quadratic equation. Therefore, the two roots of the quadratic equation x2 + 4x + 2 = 0 are x = – 2 + √2 or x = – 2 – √2