Alternate interior angles is one of an important types of angles that are formed when a transversal cuts two lines which are parallel to each other. Let us discuss alternate interior angles with the following figure.
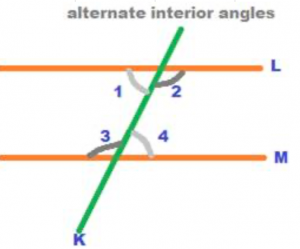
In the above figure, the two straight lines L and M are parallel to each other. This is denoted as L // M. K is a line that cuts the two parallel lines L and M. The line K is called transversal. Any line that cuts two other lines is a transversal. Among the several angles formed in the above figure only four angles have been shown numbered. The above four angles, numbered as 1, 2, 3 and 4 lie in the interior region of the parallel lines L and M. When a transversal cuts two parallel lines, then two regions are formed. They are exterior region and interior region. In the following figure, the interior region is shown in grey. The region outside the interior region of the parallel lines is called the exterior region.
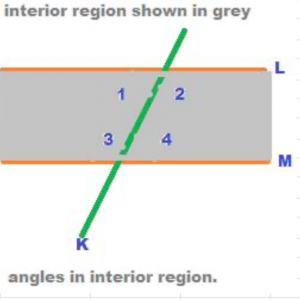
Angles formed in the interior region are called interior angles and those formed in the exterior region are called exterior angles.
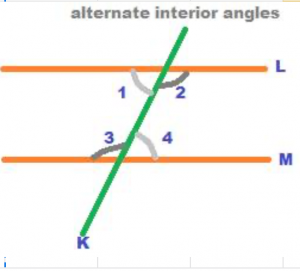
In the above figure, the four angles numbered as 1, 2, 3 and 4 are formed in the interior region of the parallel lines L and M cut by the transversal K. The four angles numbered 1, 2, 3 and 4 are hence called interior angles. Among the four interior angles in the above figure, there are two pairs of alternate angles. They are angles 1 and 4; and angles 2 and 3. The pairs of interior angles 1 and 4 are called alternate angles as they are formed on the two opposite sides of the transversal at the parallel lines. Also, since the angles are formed in the interior region, they are therefore called   alternate interior angles.
Therefore, the pairs of alternate interior angles formed in the above figure are 1 and 4; and 2 and 3.
Again, the pairs of alternate interior angles are equal to each other. So, angle 1 = angle 4, and angle 2 = angle 3.