Two angles are called complementary angles, if the sum of the degree measures of the two angles is 90.Let us discuss complementary angles with the above figure. In the above figure, we see angle ABC is a right angle. The right angle is formed at the Vertex B. A ray BD divides the right angle formed at vertex B into two parts. One part, angle ABD in the figure above, measures x degrees, while the other part, angle CBD, measures the remaining part 900 – x. The two angles, angle ABD and angle CBD are therefore called complementary angles, because the sum of the degree measures of the two angles is 90.
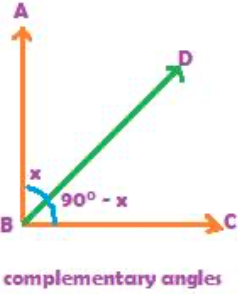
If two angles are complementary angles, then one of the two angles can be taken as x, and the other angle, as 900 – x. Each angle is described as the complement of the other. So, if x is an angle, its complement is 900 – x. Let us acquire some practice with a few questions on complementary angles:
EXAMPLE 1:
Write the complementary angles of the following angle measures
1. 300 2. 400 3. 600 4. 800
Answer:
The complement of an angle x degrees is 900 – x
So,
- the complement of 300 is 900 – 300 = 600
- the complement of 400 is 900 – 400 = 500
- the complement of 600 is 900 – 600 = 300
- the complement of 800 is 900 – 800 = 100
EXAMPLE 2:
For what degree measure of an angle, is its complement same as itself?
Answer:
Let the degree measure of the angle be x.Then the complementary angle of x is 900 – x. Since the angle = its own complement, so x = 900 – x, i.e. 2x = 900, so, x = 450
A Note:
In a right angled triangle, one angle is, of course, 900. Therefore, the other two angles in a right angled triangle are complementary angles.