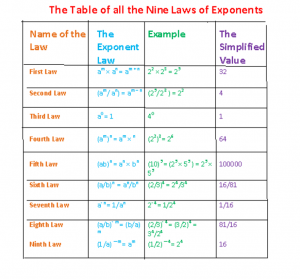
LET A BE ANY NUMBER EXCEPT 0 AND M AND N BE TWO NATURAL NUMBERS. THEN,
First Law of Exponents:
am × an = a m + n
Example 1:
32 × 33 = 32 + 3 = 35 = 243
Example 2:
24 × 24 = 28 = 256
Second Law of Exponents:
am / an = am – n
Example:
36/32 = 36 – 2 = 34 = 81
Third Law of Exponents:
If a is any number except 0, then
a0 = 1.
Example 1:
50 = 1
x0 = 1, if x is any number except 0.
Example 2:
93/93 = 93 – 3 = 90 = 1
Fourth Law of Exponents:
(am) n = (a)m × n
Example 1:
(22)3 = (2)2 × 3 = 2 6 = 64
Fifth Law of Exponents:
(ab)m = am × bm
Example 1:
(10)5 = (2 × 5)5 = 25 × 55
Sixth Law of Exponents:
(a /b) m = am/bm
Example:
(3/5)3 = 33 / 53 = 27/125. Very Important rules on exponents: (a) ?m = 1/am
Example:
(2) ?4 = 1/24 = 1/16 and (1/a) ?m = 1/ (1/a) m = am
Example:
(1/3) 4 = 34 and (a/b)- m = (b/a) m
Example:
(2/3)?4 = (3/2)4 = 34/24 = 81/16 and (am) 1/n = (am/n )
Example:
(26)1/3 = (26 ×1/3) = 26×1/3 = 22 = 4 – nth root of a number Or A Surd: Let a be a positive number and n a positive integer. Then the nth root of a is denoted as: nva or (a) 1/n and a1/n is called a Surd of order n.
Examples:
- the 2nd root of 25 is denoted as 2√25. And (25)1/2 = (52)1/2 = 52×1/2 = 52×1/2 = 5
- the 3rd root of 27 is 3√27 And (27)1/3 = (27)1/3 = (33)1/3 = 33×1/3 = 33×1/3 = 3
- The 4th root of 16 is 4√16 And 4√16 = (16)1/4 = (24)1/4 = 24×1/4 = 24×1/4 = 2
The mth root of am is m√am = (am)1/m = am×1/m = a, nth root of a negative number: let a be a negative number, then the nth root of a will exist only if n is a positive odd integer, not when n is a positive even integer.
Example:
3rd root of -8 is 3√-8, and 3√-8 = (-8)1/3 = (-23)1/3 = (-2) 3×1/3 = 23×1/3 = 2, but 2nd root of -4 does not exist, since 2 is an even integer and if the exponent is even the base can’t be negative.
Note: nth root of a positive number “a” is not defined in real numbers if n is an even integer, but nth root of the positive number “a” exists in the set of complex numbers even if n is an even integer. The Table summarizes all the laws of exponents.