What is the Midpoint formula in coordinate geometry?
Let’s consider 2 points in the XY-coordinate plane in the figure below:
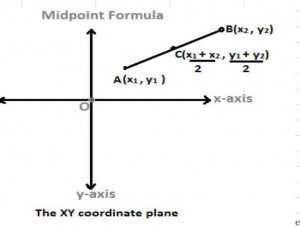
The coordinates of one point, called A is (x1, y1) and of another point, called B is (x2, y2). Let us join the two points AB with a straight line.
Let point C be the mid-point of the line segment AB, i.e. C is the point on the line segment AB that is exactly half-way from both the points A and B. In other words, it is equidistant from the two points A and B.
Then, the formula for finding the coordinates of this midpoint point C of the line segment AB formed by joining the two points A and B is
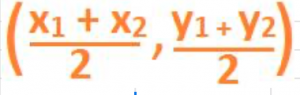
This is called the midpoint formula.
Example 1:
The two points A (2, 4) and B (6, 8) are at the opposite ends of the diameter of a circle. Find the centre of the circle.
Solution:
The centre of a circle is the midpoint of the diameter of a circle.
Applying the above midpoint formula, the centre of the circle is ((2 + 6)/2, (4 + 8)/2) which is, after simplifying, the point (4, 6).