Point slope form of equation of a straight line is used to find the equation of a straight line, when the slope of the straight line and a point through which the line is passing are given.
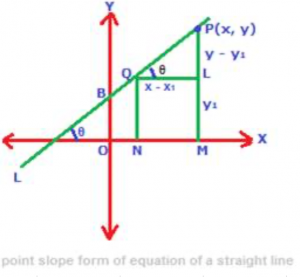
Using the above figure, let us derive below the point slope form of equation of a straight line. In the above figure, consider a straight line L which makes angle θ with the positive direction of the x-axis (i.e. x axis pointing to the right side). The angle θ is measured by moving anti-clockwise from the x axis to the straight line L which direction is considered as a positive measure of angles made by straight lines with x axis. Therefore, slope of the straight line L is tanθ, and slope is denoted by the letter m. So, m = tanθ
Again, the straight line is passing through the point Q(x1, y1). Now, for any point P(x, y) which lies on the straight line L, the locus will be the equation of the straight line L. Now, in triangle PQL, tanθ = PL/QL = (y – y1)/(x – x1) but tanθ is the slope of the straight line L and since m = tanθ, so, we get m = (y – y1)/(x – x1). After cross – multiplying, we get y – y1 = m (x – x1) this is the equation of a straight line in point slope form.
Example:
Find the equation of a straight line which is parallel to the straight line y = 4x + 5, and which is passing through the point P (2, 3)
Solution:
Equation of the straight line y = 4x + 5 is in slope intercept form y = mx + c, so slope m = 4. Again, slopes of two parallel lines are equal, therefore, slope of the required line is also 4. Substitute 2 in x1, 3 in y1 and 4 in m in point slope form y – y1 = m (x – x1) to find the equation of the required line, which will be y – 3 = 4 (x – 2). On simplifying, equation of the required straight line is y = 4x – 5.