Two angles are called supplementary angles, if the sum of their measures is 180.
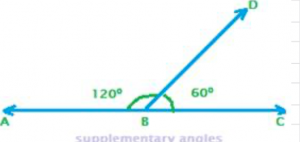
In the above figure for supplementary angles, we can see two angles formed at a common vertex B. They are angle CBD and angle ABD. Also, the sum of the two angles is 1800, which is in fact angle of a straight line. Therefore, angle CBD and angle ABD are supplementary angles. Again, each angle is said to be the supplement of the other. x and 1800 – x are collectively called supplementary angles and x is the supplement of 1800 – x, and the latter of the former too.
Example 1:
Write the supplement of the following angles: 1. 500 2. 800
The supplement of an angle x degrees is 1800 – x. Therefore, supplement of 500 is 1800 – 500 = 1300. And, supplement of 800 is 1800 – 800 = 1000
Example 2:
For what degree measure are two supplementary angles equal? Answer: If x0 is an angle, then its supplement is 1800 – x. Since the two supplementary angles are equal, so x = 180 – x, i.e. 2x = 1800. Therefore x = 900. Supplementary angles need not be adjacent angles
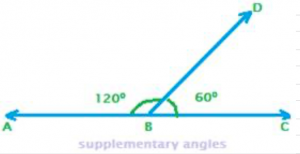
In the above figure, the two angles CBD and ABD are adjacent angles, because they are formed at a common vertex B and a common arm BD of the two angles ABD and CBD.
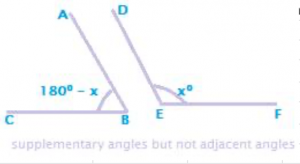
Recall that two angles are adjacent angles if they are formed at a same vertex and also if they have a common arm {ray BD}. But supplementary angles need not necessarily be adjacent angles. In the following figure, the two angles ABC and DEF are also supplementary angles, in spite of not being adjacent angles.